Skip to contents

Linear_Model_Example

Zhuoran (Angela) Yu

2025-11-04

Source: vignettes/Linear_Model_Example.Rmd
Linear_Model_Example.Rmd

The example here is to use simulated data to construct the simultaneous outer and inner confidence regions (SCRs) from simultaneous confidence bands (SCB) using linear regression. SCoRES::SCB_linear_outcome() function uses a non-parametric bootstrap algorithm to construct the SCB in linear regression. The argument df_fit specifies a data frame containing the training design matrix used to fit the linear model, while grid_df defines the mean outcome for which simultaneous confidence bands (SCB) are constructed. Use argument model to specify the formula used for fitting the linear model.

SCBs for Mean Outcome of Linear Model

In the following example, we use a linear regression to estimate the simultaneous confidence band (SCB) for the mean outcome, with modeling equation as follows:

Yi=β0+β1xi1+β2xi12+β3xi13+β4xi2+β5xi22+β6xi23+ϵi Y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i1}^2 + \beta_3 x_{i1}^3 + \beta_4 x_{i2} + \beta_5 x_{i2}^2 + \beta_6 x_{i2}^3 + \epsilon_i

We establish simultaneous confidence bands for the expected response surface E[Y|X1,X2]E[Y|X_1,X_2], with the independent variables X1X_1 and X2X_2 discretized into 100 equidistant points over the domain [−1,1][-1, 1].

library(SCoRES)
set.seed(262)
# generate simulated data
x1 <- rnorm(100)
x2 <- rnorm(100)
epsilon <- rnorm(100,0,sqrt(2))
y <- -1 + x1 + 0.5 * x1^2 - 1.1 * x1^3 - 0.5 * x2 + 0.8 * x2^2 - 1.1 * x2^3 + epsilon
df <- data.frame(x1 = x1, x2 = x2, y = y)
grid <- data.frame(x1 = seq(-1, 1, length.out = 100), x2 = seq(-1, 1, length.out = 100))
# fit the linear regression model and obtain the SCB for y
model <- "y ~ x1 + I(x1^2) + I(x1^3) + x2 + I(x2^2) + I(x2^3)"
results <- SCB_linear_outcome(df_fit = df, model = model, grid_df = grid)

The levels = c(-0.3, 0, 0.3) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plots the estimated inverse regions, the inner confidence regions, and the outer confidence regions.

results <- tibble::as_tibble(results)
suppressWarnings(plot_cs(results,
        levels = c(-0.3, 0, 0.3), 
        x = seq(-1, 1, length.out = 100), 
        mu_hat = results$Mean, 
        xlab = "x1", 
        ylab = "y", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black"))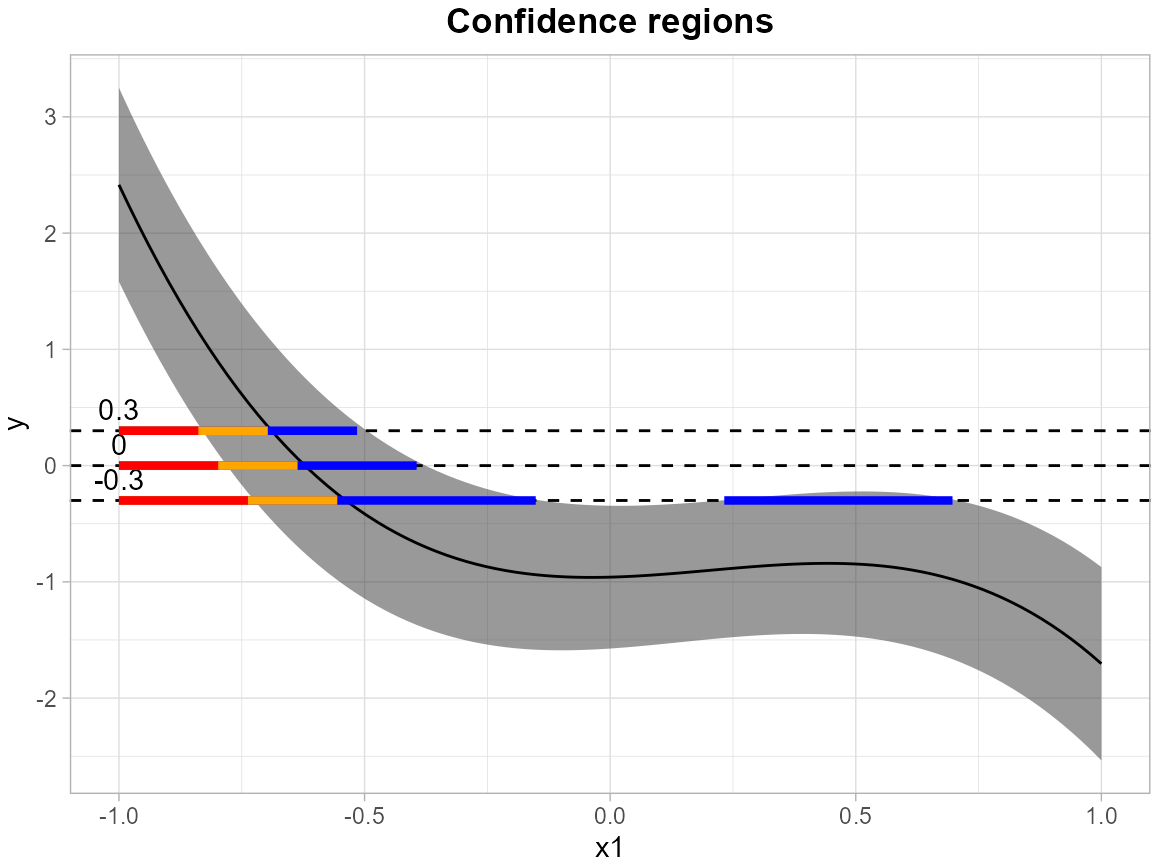

In the following example, we establish simultaneous confidence bands for the expected response surface E[Y|X1,X2=0]E[Y|X_1, X_2 =0], with the independent variable X1X_1 discretized into 100 equidistant points over the domain [−1,1][-1, 1].

x1 <- rnorm(100)
x2 <- rnorm(100)
epsilon <- rnorm(100,0,sqrt(2))
y <- -1 + x1 + 0.5 * x1^2 - 1.1 * x1^3 - 0.5 * x2 + 0.8 * x2^2 - 1.1 * x2^3 + epsilon
df <- data.frame(x1 = x1, x2 = x2, y = y)
# fit the linear regression model and obtain the SCB for y
model <- "y ~ x1 + I(x1^2) + I(x1^3) + x2 + I(x2^2) + I(x2^3)"
grid <- data.frame(x2 = seq(-1, 1, length.out = 100))
results <- SCB_linear_outcome(df_fit = df, model = model, grid_df = grid)

The levels = c(-1.5, -1.0, -0.5) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plots the estimated inverse regions, the inner confidence regions, and the outer confidence regions.

results <- tibble::as_tibble(results)
suppressWarnings(plot_cs(results,
        levels = c(-1.5, -1.0, -0.5), 
        x = seq(-1, 1, length.out = 100), 
        mu_hat = results$Mean, 
        xlab = "x2", 
        ylab = "y", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black"))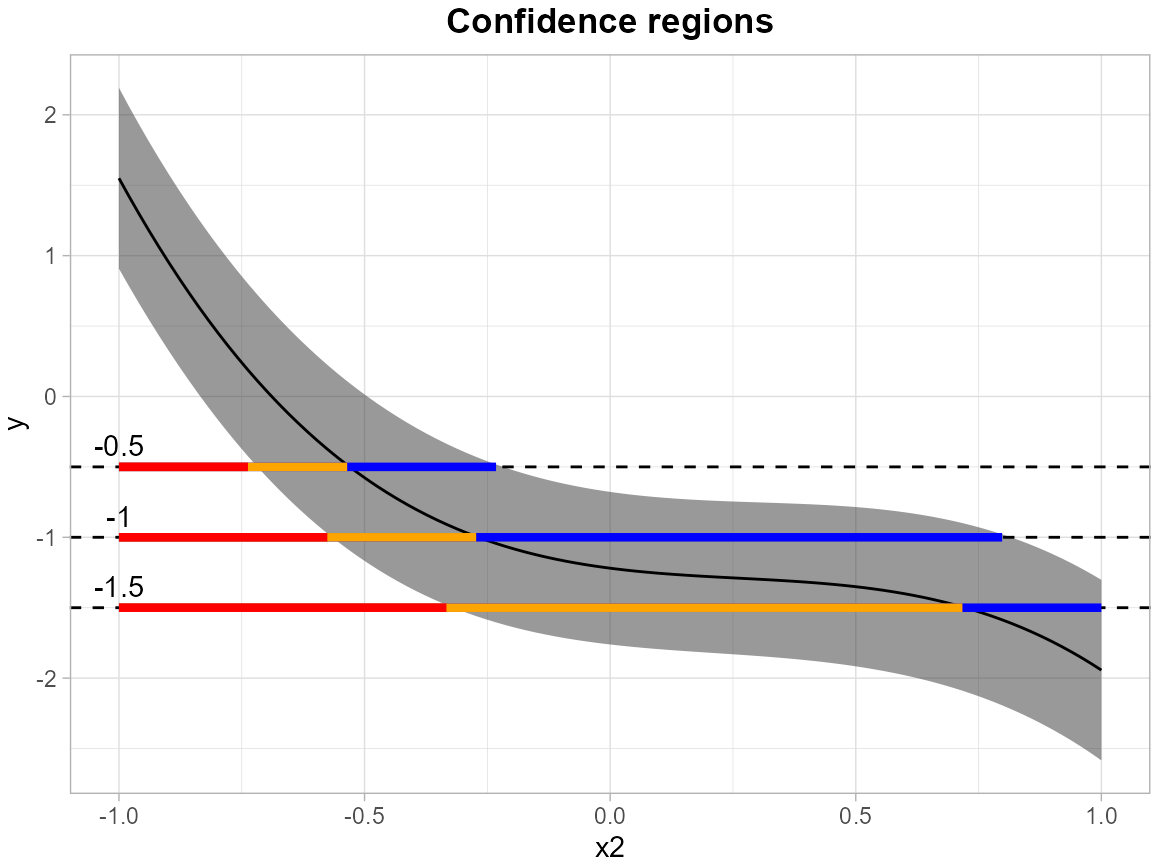

SCBs for Mean Outcome of Logistic Model

In addition to linear regression, SCoRES also providesSCoRES::SCB_logistic_outcome() for estimating the SCB for outcome of logistic regression.

Here, we use a similar model structure with logistic regression to estimate the simultaneous confidence band (SCB) for the outcome probability, with modeling equation as follows:

Yi∼Bernoulli(pi) Y_i \sim Bernoulli(p_i) log(pi1−pi)=β0+β1xi1+β2xi12+β3xi13+β4xi2+β5xi22+β6xi23 \log\left(\frac{p_i}{1-p_i}\right) = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i1}^2 + \beta_3 x_{i1}^3 + \beta_4 x_{i2} + \beta_5 x_{i2}^2 + \beta_6 x_{i2}^3

We establish simultaneous confidence bands for the expected response surface logit(E[Y|X1,X2])\text{logit}(E[Y|X_1,X_2]), with the independent variables X1X_1 and X2X_2 discretized into 100 equidistant points over the domain [−1,1][-1, 1].

# generate simulated data
x1 <- rnorm(100)
x2 <- rnorm(100)
mu <- -1 + x1 + 0.5 * x1^2 - 1.1 * x1^3 - 0.5 * x2 + 0.8 * x2^2 - 1.1 * x2^3
p <- expit(mu)
y <- rbinom(100, size = 1, prob = p)
df <- data.frame(x1 = x1, x2 = x2, y = y)
grid <- data.frame(x1 = seq(-1, 1, length.out = 100), x2 = seq(-1, 1, length.out = 100))
# fit the logistic regression model and obtain the SCB for y
model <- "y ~ x1 + I(x1^2) + I(x1^3) + x2 + I(x2^2) + I(x2^3)"
results <- SCB_logistic_outcome(df_fit = df, model = model, grid_df = grid)

Likewise, the levels = c(0.3, 0.4, 0.5) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plot the estimated inverse region, the inner confidence region, and the outer confidence region.

results <- tibble::as_tibble(results)
plot_cs(results,
        levels = c(0.3, 0.4, 0.5), 
        x = seq(-1, 1, length.out = 100), 
        mu_hat = results$Mean, 
        xlab = "x1", 
        ylab = "y", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")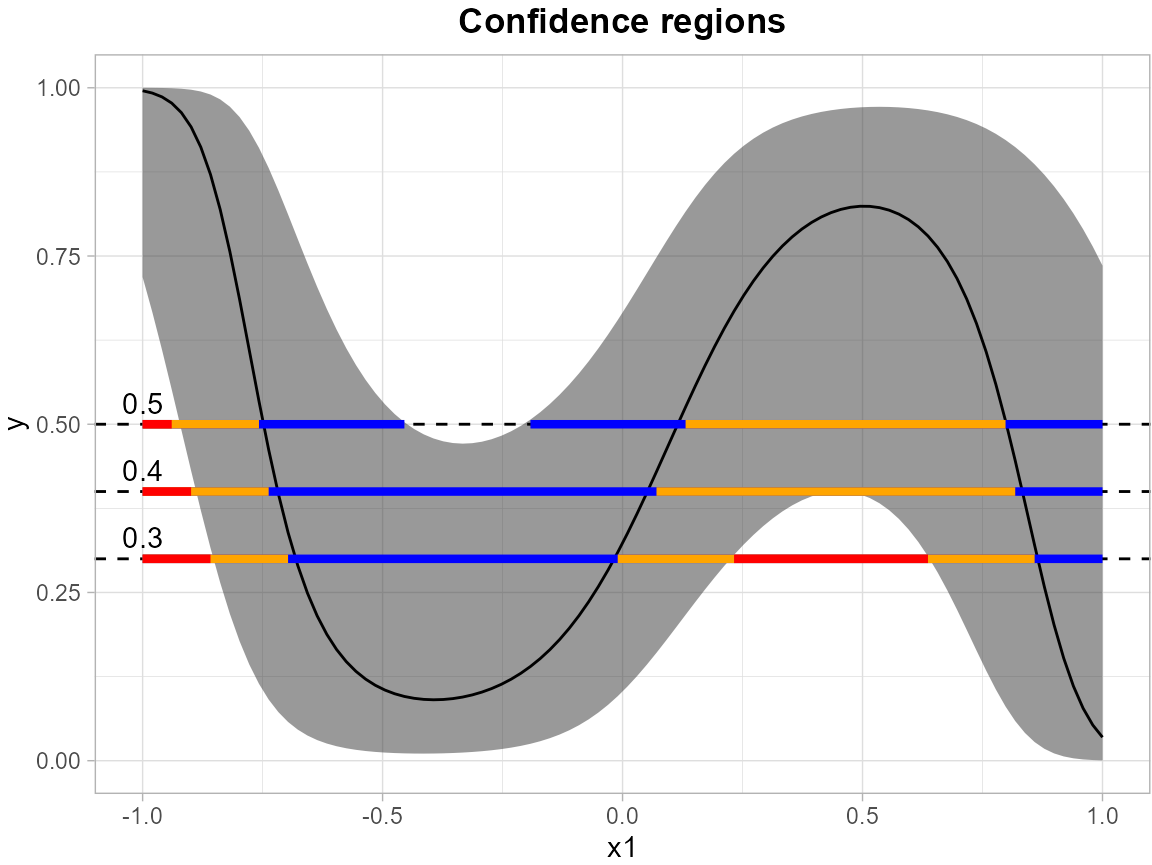

SCBs for Coefficients of Linear/Logistic Model

Besides, SCoRES::SCB_regression_coef can estimate the SCB for every coefficient in the linear/logistic model.

Here, we use a linear regression model with 50 coefficients in total to estimate the simultaneous confidence band (SCB) for all coefficients and the intercept, with modeling equation as follows: Yi=β0+∑j=150Xijβj+ϵi, Y_i = \beta_0 + \sum^{50}_{j=1}X_{ij}\beta_j + \epsilon_i, where Cov(Xi,Xj)=0.4|i−j|Cov(X_i, X_j)=0.4^{|i-j|}.

library(MASS)
# generate simulated data
M <- 50
rho <- 0.4
n <- 500
beta <- rnorm(M, mean = 0, sd = 1)
Sigma <- outer(1:M, 1:M, function(i, j) rho^abs(i - j))
X <- MASS::mvrnorm(n = n, mu = rep(0, M), Sigma = Sigma)
epsilon <- rnorm(n, mean = 0, sd = 1)
y <- X %*% beta + epsilon
df <- as.data.frame(X)
names(df) <- paste0(1:M)
df$y <- as.vector(y)
# fit the linear regression model and obtain the SCB for all betas
model <- "y ~ ."
results <- SCB_regression_coef(df, model)

Likewise, the levels = c(-2, -0.5, -0.1, 0.2) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plots the estimated inverse regions, the inner confidence regions, and the outer confidence regions.

results <- tibble::as_tibble(results)
plot_cs(results,
        levels = c(-2, -0.5, -0.1, 0.2), 
        x = c("intercept", as.character(1:50)), 
        mu_hat = results$Mean, 
        xlab = "Coefficients", 
        ylab = "SCBs for Coefficients", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")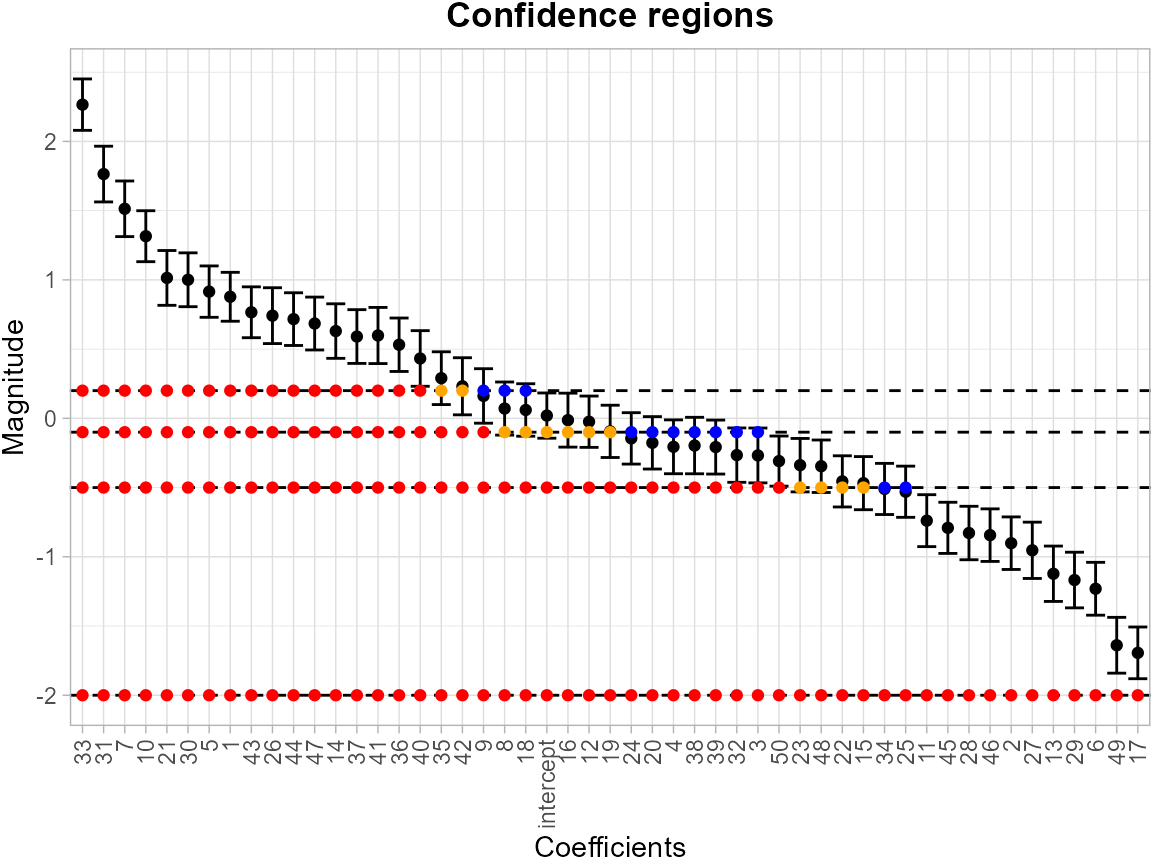

Users can also compute the SCB for any linear combination of these coefficients by specifying a weight vector of the same length as the coefficient vector. This can be done by using SCoRES::SCB_regression_outcome(), and specifying the linear combination through w. For example, suppose we want to calculate the SCB for the linear combination β1+β2+β3\beta_1+\beta_2+\beta_3 for model: y=β0+β1X1+β2X12+β3X13+β4X2+β5X22+β6X32y=\beta_0+\beta_1 X_1 +\beta_2X^2_1+\beta_3X^3_1+\beta_4X_2+\beta_5X^2_2+\beta_6X^2_3:

x1 <- rnorm(100)
x2 <- rnorm(100)
epsilon <- rnorm(100,0,sqrt(2))
y <- -1 + x1 + 0.5 * x1^2 - 1.1 * x1^3 - 0.5 * x2 + 0.8 * x2^2 - 1.1 * x2^3 + epsilon
df <- data.frame(x1 = x1, x2 = x2, y = y)
grid <- data.frame(x1 = seq(-1, 1, length.out = 100), x2 = seq(-1, 1, length.out = 100))
# fit the linear regression model and obtain the SCB for y
model <- "y ~ x1 + I(x1^2) + I(x1^3) + x2 + I(x2^2) + I(x2^3)"
w <- matrix(c(0, 1, 1, 1, 0, 0, 0), ncol = 7)

SCB_regression_outcome(df_fit = df, model = model,
                       grid_df = grid, n_boot = 50, alpha = 0.1,
                       fitted = FALSE, w = w)
#>            scb_low      Mean   scb_up
#> scb_low -0.4971322 0.3964766 1.290085

In the following example, we load ipad dataset, and establish simultaneous confidence bands for all the coefficients and the intercept in the model fitted. Here, we set log(t_mmr1) as the outcome, and include all variables from Pupillography, Tablet (task metrics) and Cardiovascular as predictors.

library(SCoRES)
library(dplyr)
library(ggplot2)
set.seed(262)
data(ipad)
df <- ipad %>%
  filter(t_mmr1 > 0) %>%
  select(p_fpc1, p_fpc2, p_fpc3, p_fpc4, p_fpc5, p_fpc6,
         p_PMC_pctChg, p_auc, t_mmr1,
         i_prop_false_timeout, i_prop_failed1, i_prop_failed2, 
         i_judgement_time1, i_judgement_time2, i_time_outside_reticle, 
         i_time_on_edge, i_prop_hit, i_correct_reaction2, 
         i_reaction_time_max2, i_reaction_time2, i_rep_shapes12, 
         i_rep_shapes34, i_memory_time12, i_memory_time34, 
         i_composite_score, h_hr, h_dbp, h_sbp, recent_smoke) %>%
  mutate(log_tmmr1 = log(t_mmr1))
df_lin <- df %>%
  select(-recent_smoke, -t_mmr1)
# fit the linear regression model and obtain the SCB for y
model_lin <- "log_tmmr1 ~ ."
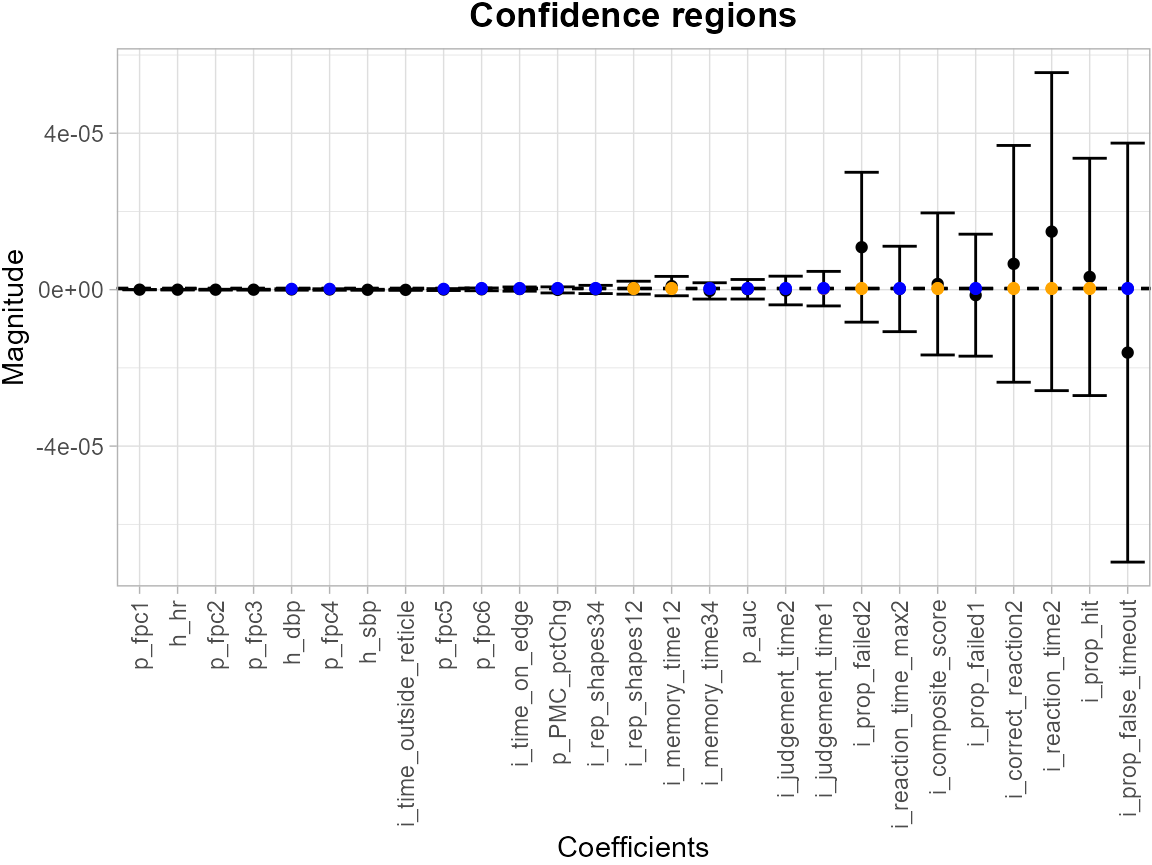
results <- SCB_regression_coef(df_fit = df_lin, model = model_lin)

The levels = c(0.2, 0.3, 0.4) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plot the estimated inverse region, the inner confidence region, and the outer confidence region. Here, for illustration, we filter out the SCB for intercept.

results <- tibble::as_tibble(results[-1, ])
suppressWarnings(plot_cs(results,
        levels = c(0.2, 0.3, 0.4), 
        x = c(names(df_lin)[1:(length(names(df_lin))-1)]), 
        mu_hat = results$Mean, 
        xlab = "", 
        ylab = "", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black"))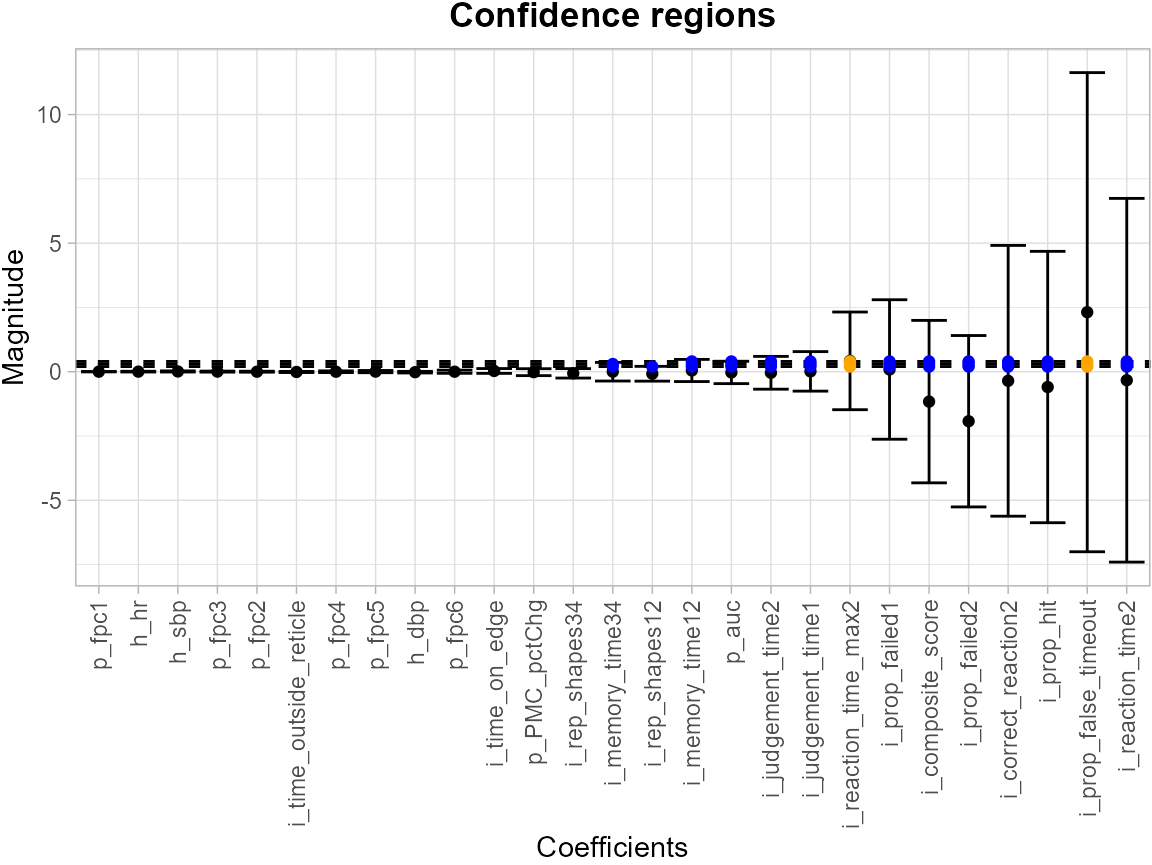

We fit a logistic model with recent_smoke as outcome with the same predictors in linear regression model, and obtain SCBs for all coefficients and the intercept.

df_log <- df %>%
  select(-t_mmr1, -log_tmmr1)
# fit the logistic regression model and obtain the SCB for y
model_log <- "recent_smoke ~ ."
results <- SCB_regression_coef(df_fit = df_log, model = model_log, type = "logistic")

The levels = c(2e-07, 3e-07, 4e-07) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plots the estimated inverse regions, the inner confidence regions, and the outer confidence regions. Here, for illustration, we filter out the SCB for intercept.

results <- tibble::as_tibble(results[-1, ])
suppressWarnings(plot_cs(results,
        levels = c(2e-07, 3e-07, 4e-07), 
        x = c(names(df_log)[1:(length(names(df_log))-1)]), 
        mu_hat = results$Mean, 
        xlab = "", 
        ylab = "", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black"))