Skip to contents

Functional_Data_Example

Zhuoran (Angela) Yu

2025-11-04

Source: vignettes/Functional_Data_Example.Rmd
Functional_Data_Example.Rmd

Overview

The example here is to use pupil functional data to construct the simultaneous outer and inner confidence regions (SCRs) from simultaneous confidence bands (SCBs) using Function-on-Scalar Regression (FoSR).

The pupil dataset contains repeated measures of percent change over time for multiple subjects under two user categories (use: 1 and no use: 0). It contains both user and non-user groups, multiple time points, and several covariates, including age, gender, BMI, and alcohol consumption.

library(SCoRES)
library(mgcv)
data(pupil)

Before calculating the SCBs, we first process pupil data by fitting a mean GAM model, extracting residuals and performing FPCA using SCoRES::prepare_pupil_fpca(), the function will return an enhanced dataset that includes the FPCA-derived basis scores (Phi1, Phi2, Phi3, Phi4) for Function-on-Scalar Regression (FoSR) analysis.

Following the FPCA-based data augmentation, we fit a FoSR model using mgcv::bam(), which allows efficient estimation of Generalized Additive Mixed Models (GAMMs). The model formula is designed to capture both population-level smooth trends and subject-specific functional variation.

The response here is percent_change. Time variable t is seconds, and the covariate is use, which is a binary indicator (1:use, 0:no use).

The function-on-scalar regression model is

percent_changei(t)=β0(t)+β1(t)usei+bi(t)+ϵi(t), \text{percent_change}_i(t) = \beta_0(t) + \beta_1(t) \text{use}_i + b_i(t) + \epsilon_i(t), 

pupil_fpca <- SCoRES::prepare_pupil_fpca(pupil)
fosr_mod <- mgcv::bam(percent_change ~ s(seconds, k=30, bs="cr") +
            s(seconds, by = use, k=30, bs = "cr") +
            s(id, by = Phi1, bs="re") +
            s(id, by = Phi2, bs="re") +
            s(id, by = Phi3, bs="re") +
            s(id, by = Phi4, bs="re"),
            method = "fREML", data = pupil_fpca, discrete = TRUE)

After obtaining the FoSR object fosr_mod, the simultaneous confidence bands (SCBs) can be constructed through SCoRES::SCB_functional_outcome using pre-specified methods. The SCoRES package provides two options for calculating simultaneous confidence bands (SCBs), specified via the method argument: cma: Correlation and Multiplicity Adjusted (CMA) confidence bands via parametric approach from Crainiceanu et al. (2024). multiplier: Dense confidence bands via Multiplier-t Bootstrap method from Telschow & Schwartzman (2022). Use subset to specify the names of grouping variables to analyze. The input data should have numerical binary 0/1 values for all scalar group variables. Here, we analyze the user group by specifying subset = c("use = 1"). Use fitted to specify the object for SCB estimation. If fitted = TRUE, SCoRES::SCB_functional_outcome will construct the SCB for the fitted mean outcome function. If fitted = FALSE, SCoRES::SCB_functional_outcome will construct the SCB for the fitted parameter function. For cma option, users are required to provide a functional regression object through argument object. For multiplier option, users also need to provide input for object. If object = NULL, the function will only output the SCB for an overall mean outcome function regardless of the group specified.

Here, we estimate SCBs using both options separately for the mean outcome Y(t) of user’s group: E[percent_change(t)|use=1]=β0(t)+β1(t), E[\text{percent_change}(t) | \text{use} = 1] = \beta_0(t) + \beta_1(t),

In the multiplier bootstrap procedure, SCoRES supports three types of multiplier distributions, which is specified by weights:

  • "rademacher": gi∈{−1,+1}g_i \in \{-1, +1\} with equal probability
  • "gaussian": gi∼𝒩(0,1)g_i \sim \mathcal{N}(0, 1)
  • "mammen": A two-point distribution with mean zero and variance one (see Mammen, 1993)

Default is rademacher.

Two options are available for estimating the standard error ϵ̂N*(sj)\hat{\epsilon}_N^*(s_j), which is specified by method_SD:

  • “regular” (empirical standard error based on residuals):

  • “t” (bootstrap second moment-based estimator):

Default is t.

For mathematical details, see vignette Methods.

Correlation and Multiplicity Adjusted (CMA) Confidence Bands

SCB for Mean Outcome Function

The code below visualizes the simultaneous outer and inner regions derived from SCB results using the SCoRES::plot_cs() function. The results object is first converted to a tibble for easier manipulation.

The levels = c(-18, -20, -22, -24) argument specifies a set of thresholds, and SCoRES::plot_cs() function estimates multiple inverse upper excursion sets corresponding to these thresholds, and plots the estimated inverse regions, the inner confidence regions, and the outer confidence regions.

# CMA approach
results_pupil_cma <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          object = fosr_mod, 
                                          method = "cma",
                                          fitted = TRUE, 
                                          alpha = 0.05, 
                                          outcome = "percent_change",
                                          domain = "seconds", 
                                          subset = c("use = 1"), 
                                          id = "id")

results_pupil_cma <- tibble::as_tibble(results_pupil_cma)
plot_cs(results_pupil_cma,
        levels = c(-18, -20, -22, -24), 
        x = results_pupil_cma$domain, 
        mu_hat = results_pupil_cma$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
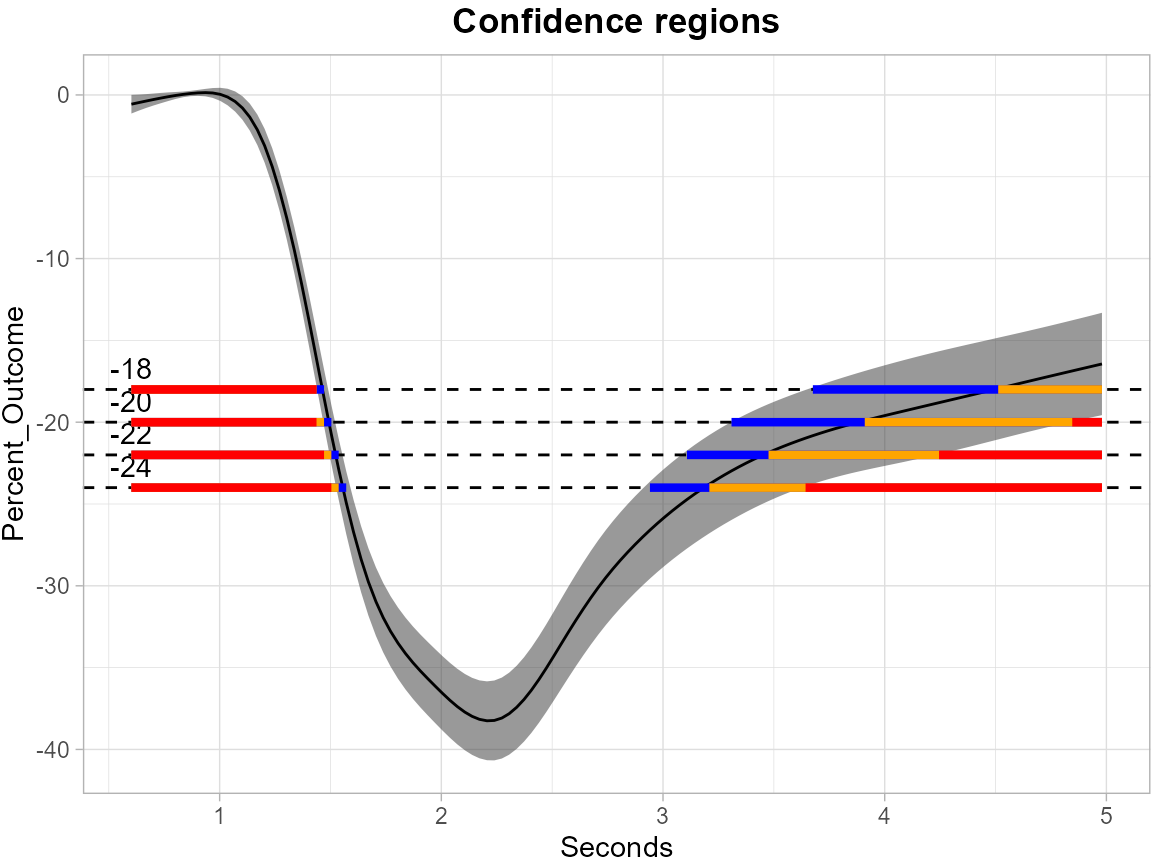
        color_level_label = "black")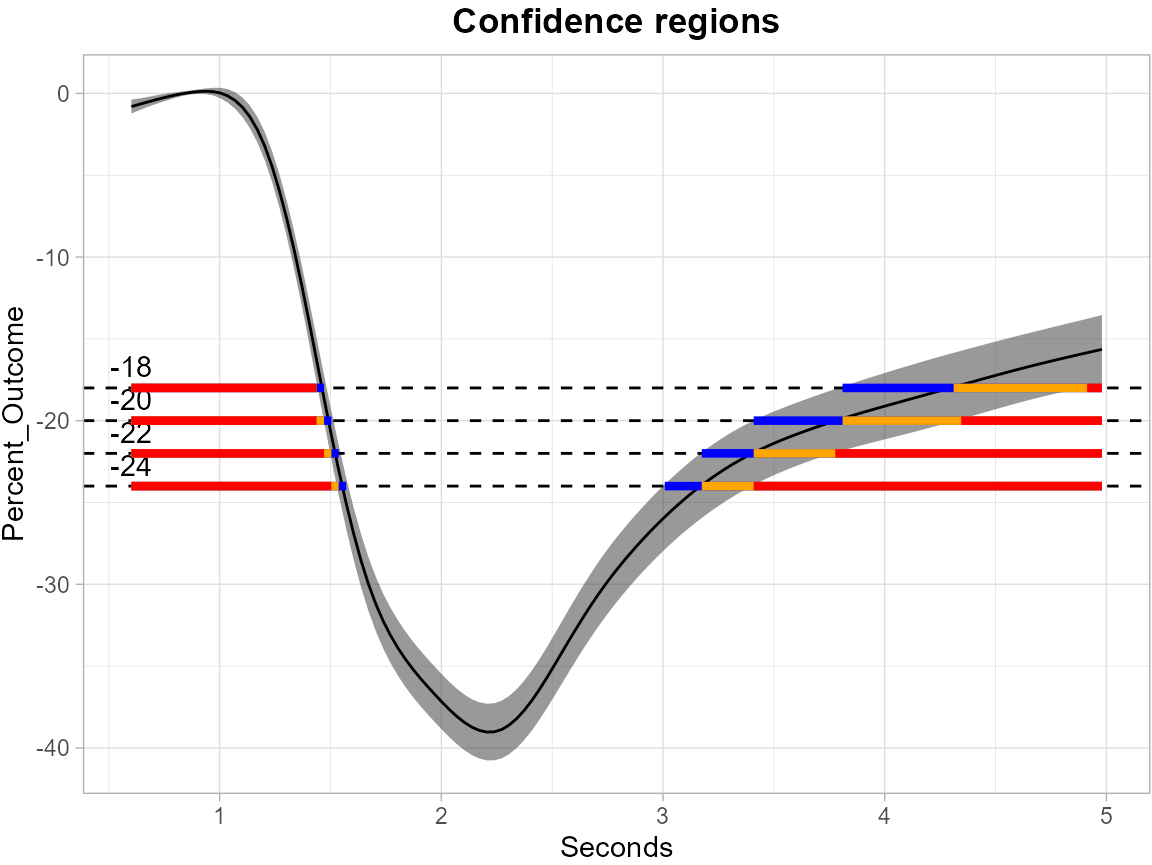

The plot demonstrates how to use SCBs to find regions of time where the estimated mean is greater than or equal to the four levels -18, -20, -22 and -24 for pupil data. The gray shaded area is the 95% SCB, the solid black line is the estimated mean. The red horizontal line shows the inner confidence regions (where the lower SCB is greater than the corresponding level) that are contained in the estimated inverse region represented by the union of the yellow and red horizontal line (where the estimated mean is greater than the corresponding levels); the outer confidence regions are the union of the blue, yellow and red line (where the upper SCB is greater than the corresponding levels) and contain both the estimated inverse regions and the inner confidence regions.

SCB for Coefficient Function

The next plot shows the SCB for the coefficient function for the use group, and the corresponding SCRs based on specified levels.

#CMA approach for parameter function
results_pupil_cma_para <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          object = fosr_mod, 
                                          method = "cma",
                                          fitted = FALSE, 
                                          alpha = 0.05, 
                                          outcome = "percent_change",
                                          domain = "seconds", 
                                          subset = c("use = 1"), 
                                          id = "id")

results_pupil_cma_para <- tibble::as_tibble(results_pupil_cma_para)
plot_cs(results_pupil_cma_para,
        levels = c(4.5, 5, 5.5, 6), 
        x = results_pupil_cma_para$domain, 
        mu_hat = results_pupil_cma_para$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")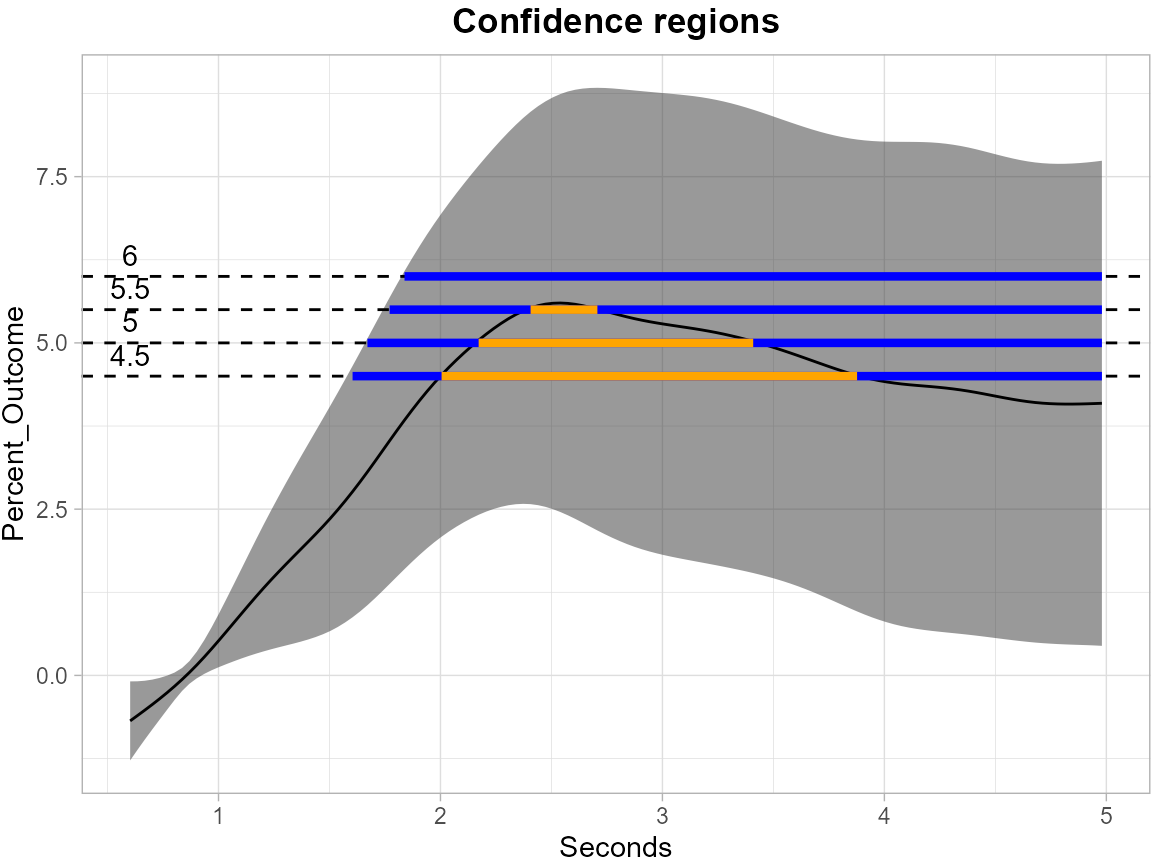

Multiplier-t Bootstrap Confidence Bands

SCB for Mean Outcome Function

The following plots show the results of multiplier bootstrap. The first one displays the SCB for mean outcome function for the use group, while the second one is for the coefficient function of the use group. All possible NA’s are imputed using refund::fpca.face().

# Multiplier-t Bootstrap
results_pupil_multiplier <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          object = fosr_mod, 
                                          method = "multiplier",
                                          fitted = TRUE, 
                                          alpha = 0.05, 
                                          outcome = "percent_change",
                                          domain = "seconds", 
                                          subset = c("use = 1"), 
                                          id = "id")

results_pupil_multiplier <- tibble::as_tibble(results_pupil_multiplier)
plot_cs(results_pupil_multiplier,
        levels = c(-18, -20, -22, -24), 
        x = results_pupil_multiplier$domain, 
        mu_hat = results_pupil_multiplier$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome",
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")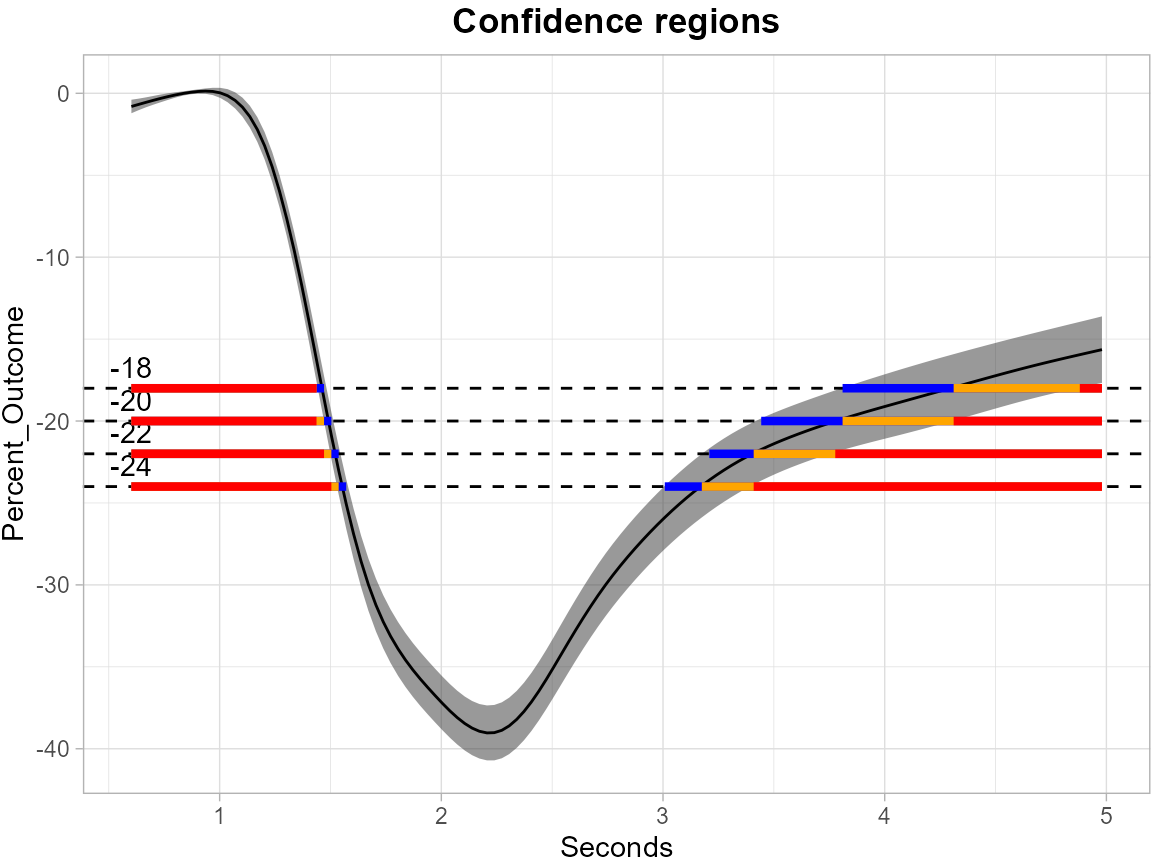

SCB for Coefficient Function 

results_pupil_multiplier_para <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          object = fosr_mod, 
                                          method = "multiplier",
                                          fitted = FALSE, 
                                          alpha = 0.05, 
                                          outcome = "percent_change",
                                          domain = "seconds", 
                                          subset = c("use = 1"), 
                                          id = "id")

results_pupil_multiplier_para <- tibble::as_tibble(results_pupil_multiplier_para)
plot_cs(results_pupil_multiplier_para,
        levels = c(4.5, 5, 5.5, 6), 
        x = results_pupil_multiplier_para$domain, 
        mu_hat = results_pupil_multiplier_para$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome",
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")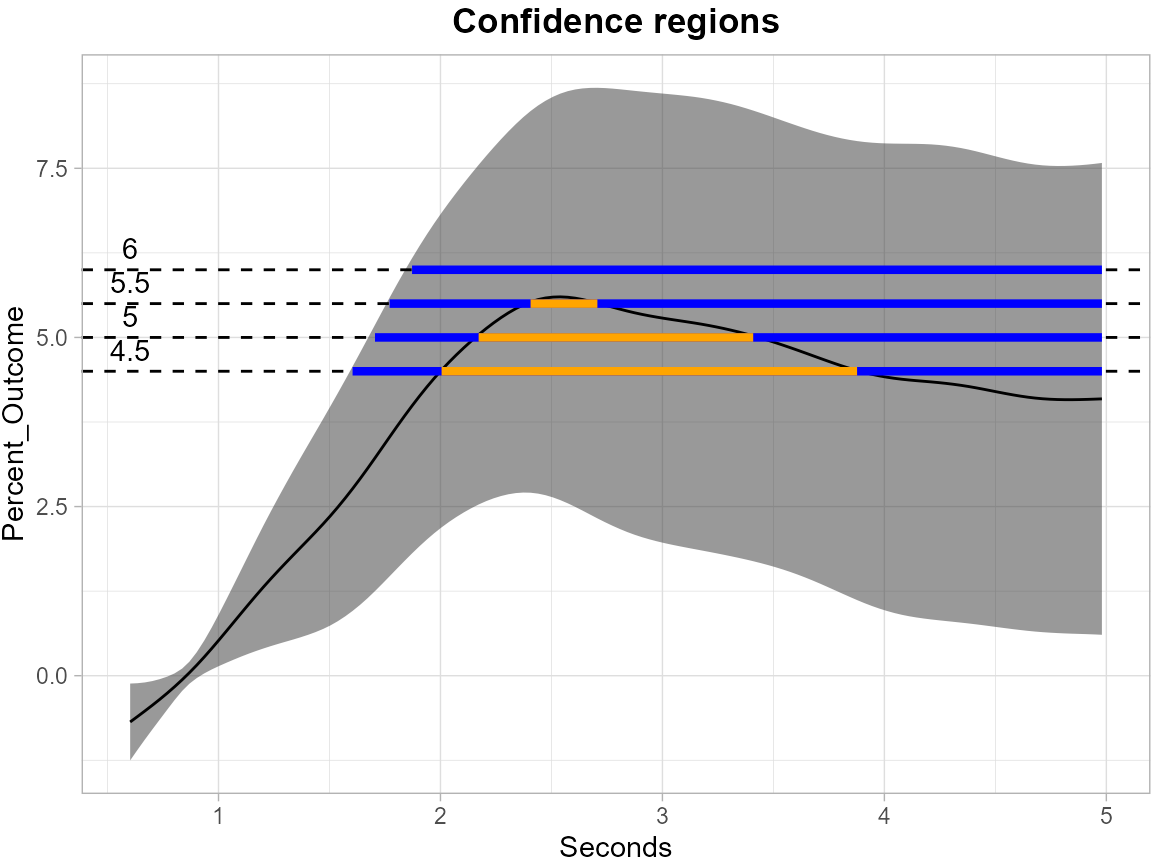

The following plot displays the SCB and the corresponding SCRs of specified levels for the overall mean outcome function. The solid black line represents the sample mean.

results_pupil_multiplier_overall <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          method = "multiplier",
                                          fitted = TRUE,
                                          alpha = 0.05, 
                                          outcome = "percent_change",
                                          domain = "seconds", 
                                          subset = c("use = 1"), 
                                          id = "id")
#> [1] "No Functional Regression Object provided, will only compute an overall SCB for the outcome regardless of the group specified."

results_pupil_multiplier_overall <- tibble::as_tibble(results_pupil_multiplier_overall)
plot_cs(results_pupil_multiplier_overall,
        levels = c(-18, -20, -22, -24), 
        x = results_pupil_multiplier_overall$domain, 
        mu_hat = results_pupil_multiplier_overall$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome", 
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")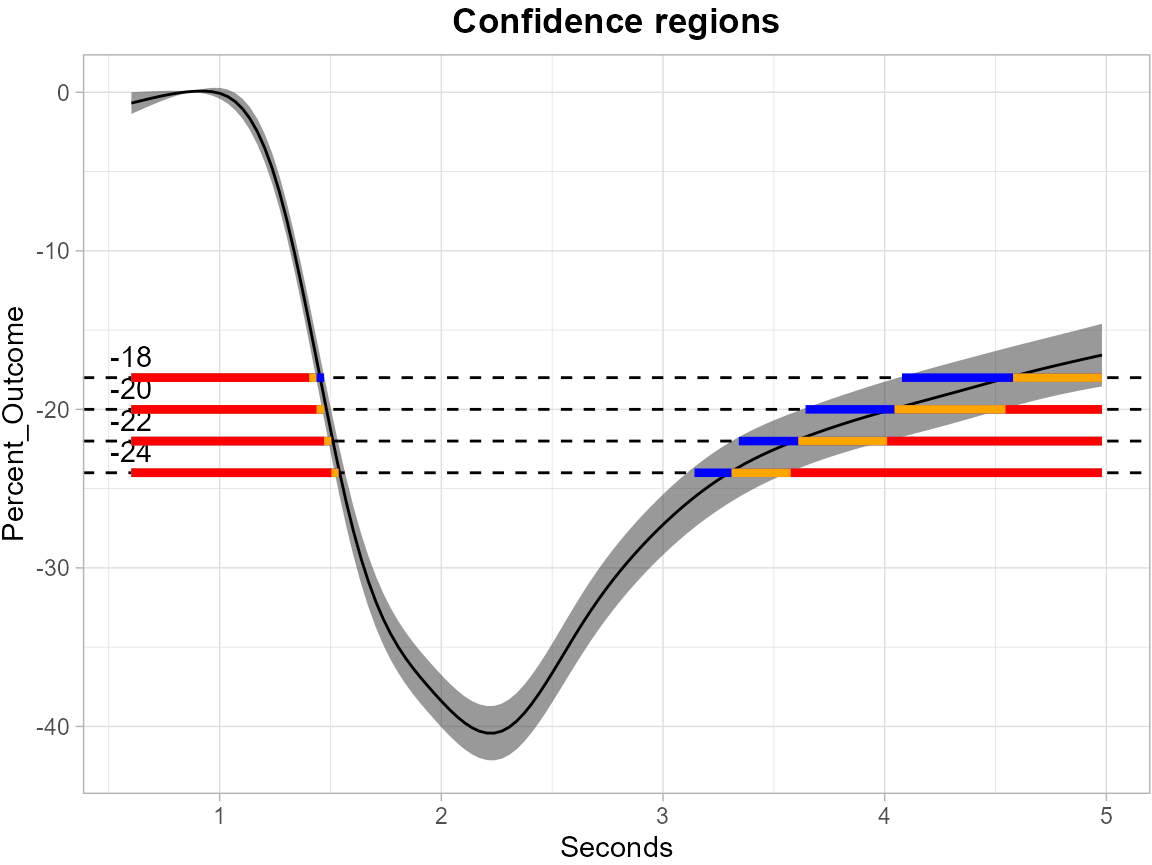

An Extended Example

Correlation and Multiplicity Adjusted (CMA) Confidence Bands

SCB for Mean Outcome Function

To further illustrate the power of SCoRES::SCB_functional_outcome for constructing SCBs for multiple group variables, we add age and gender as covariates, and analyze the 40-year-old male user group by specifying group_name = c("use", "age", "gender") and group_value = c(1, 40, 0). We set fitted = TRUE.

The function-on-scalar regression model is

percent_changei(t)=β0(t)+β1(t)usei+β2(t)agei+β3(t)genderi+bi(t)+ϵi(t), \text{percent_change}_i(t) = \beta_0(t) + \beta_1(t) \text{use}_i + \beta_2(t) \text{age}_i + \beta_3(t) \text{gender}_i + b_i(t) + \epsilon_i(t), 

pupil_fpca <- SCoRES::prepare_pupil_fpca(pupil, example = "extended")
fosr_mod <- mgcv::bam(percent_change ~ s(seconds, k=30, bs="cr") +
            s(seconds, by = use, k=30, bs = "cr") +
            s(seconds, by = age, k = 30, bs = "cr") +
            s(seconds, by = gender, k = 30, bs = "cr") +
            s(id, by = Phi1, bs="re") +
            s(id, by = Phi2, bs="re") +
            s(id, by = Phi3, bs="re") +
            s(id, by = Phi4, bs="re"),
            method = "fREML", data = pupil_fpca, discrete = TRUE)

The SCBs are estimated using both options separately for the mean outcome Y(t) of the specified group:

E[percent_change(t)|use=1,age=40,gender=0]=β0(t)+β1(t)+40*β2(t), E[\text{percent_change}(t) | \text{use} = 1, \text{age} = 40, \text{gender} = 0]= \beta_0(t) + \beta_1(t) + 40*\beta_2(t),

The following plots show the SCBs and inverse SCBs for the mean outcome function. The first one is from CMA approach and the second is from multiplier bootstrap.

# CMA approach
results_pupil_cma <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          object = fosr_mod, 
                                          method = "cma", 
                                          fitted = TRUE,
                                          alpha = 0.05, 
                                          outcome = "percent_change", 
                                          domain = "seconds", 
                                          subset = c("use = 1", 
                                                     "age = 40", 
                                                     "gender = 0"),  
                                          id = "id")

results_pupil_cma <- tibble::as_tibble(results_pupil_cma)
plot_cs(results_pupil_cma,
        levels = c(-18, -20, -22, -24), 
        x = results_pupil_cma$domain, 
        mu_hat = results_pupil_cma$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome",
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")

Multiplier-t Bootstrap Confidence Bands

SCB for Mean Outcome Function 

# Multiplier-t Bootstrap
results_pupil_multiplier <- SCoRES::SCB_functional_outcome(
                                          data_df = pupil,
                                          object = fosr_mod,
                                          fitted = TRUE,
                                          method = "multiplier", 
                                          alpha = 0.05, 
                                          outcome = "percent_change", 
                                          domain = "seconds", 
                                          subset = c("use = 1", 
                                                     "age = 40", 
                                                     "gender = 0"), 
                                          id = "id")

results_pupil_multiplier <- tibble::as_tibble(results_pupil_multiplier)
plot_cs(results_pupil_multiplier,
        levels = c(-18, -20, -22, -24), 
        x = results_pupil_multiplier$domain, 
        mu_hat = results_pupil_multiplier$mu_hat, 
        xlab = "Seconds", 
        ylab = "Percent_Outcome",
        level_label = T, 
        min.size = 40, 
        palette = "Spectral", 
        color_level_label = "black")

Crainiceanu, C. M., Goldsmith, J., Leroux, A., & Cui, E. (2024). Functional data analysis with r. Chapman; Hall/CRC.
Telschow, F. J. E., & Schwartzman, A. (2022). Simultaneous confidence bands for functional data using the gaussian kinematic formula. Journal of Statistical Planning and Inference, 216, 70–94. https://doi.org/10.1016/j.jspi.2021.05.008